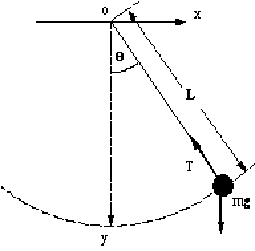
振幅の大きな振り子
運動方程式
上図のようにパラメターを設定する．運動方程式は、
と書ける．（教科書を参考）
問１ 上の方程式をニュートンの第二法則から導き出せ．
θ が十分小さい
まず、θ が十分小さいとして、この方程式を解いてみよう．
In[1]:=
Out[1]=
であるから、第一項だけをとり微分方程式を解く．ただし、初期条件としてt=0のときθ[0]==Θ, θ'[0]==0であるとする．
In[2]:=
Out[2]=
問２
（１）上の解より、振りの角度θが小さい時、振り子はどのような運動をするといえるか．
（２）また、その周期は何か．
問３ Taylor 展開は上の例で分かるようにSeriesを用いればよい．例えば、
In[3]:=
Out[3]=
上の例では0の周りで展開したが、x=1の周りで展開したいときは、
In[4]:=
Out[4]=
とすればよい．
次の関数を0の周りでx^10のオーダーまで求めよ・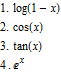
5. tanh(x)
6. 
θ が一般の場合
運動の周期に関する議論は教科書をみてください．ここでは微分方程式を数値的に解いて、相空間図を描くことにする．まず
In[5]:=
と仮定し（もちろん、数値計算では全てのパラメターに数字を代入しなければならない）、
Θ=Pi/3;
まずΘ=π/3として計算してみよう．
In[7]:=
Out[7]=
In[8]:=
Out[8]=
注意：
In[9]:=
角度と振幅の図を描く．
In[10]:=
Out[10]=
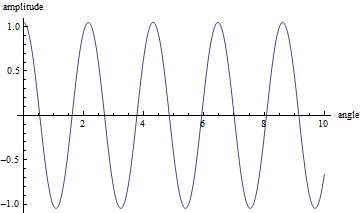
角速度と振幅の図を描く．
In[11]:=
Out[11]=
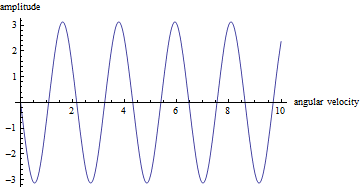
角度と角速度の相空間図を描きg1と名付ける．
In[12]:=
Out[12]=
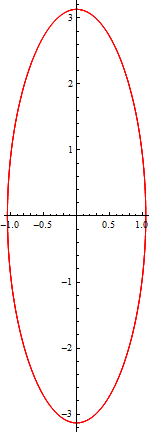
この結果と上の単振動の結果を相空間でどのように違うか、見てみよう．同じ初期条件でプロットすると、
In[13]:=
Out[13]=
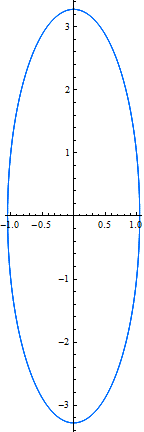
この二つの結果を一つのグラフにする．
In[14]:=
Out[14]=
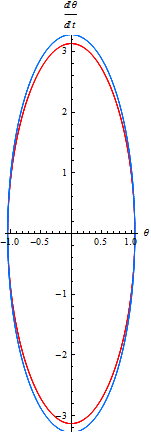
問４上のグラフからどのようなことがいえるか．(なぜ上の二つの軌道は一致しないのか？）
問５ NDSolve を使って以下の微分方程式を解け．
例
を
y(0)==1
として、0<x<10 の間で解いてみよう．
In[15]:=
Out[15]=
この結果を使うには、例えば
In[16]:=
Out[16]=
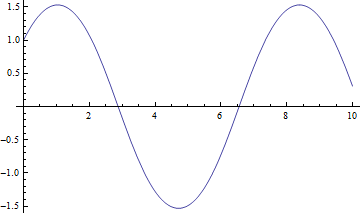
とすれば、グラフが得られるし、x=0.5の時のyの値がほしければ
In[17]:=
Out[17]=
というようにできる．
(1)
を
y(0)==1
として、-3Pi<x<3Pi の間で数値的に解いてグラフを描け．（解答用紙にプリントアウトを切り取ってはっても良いし、スケッチ的に書いても良い．）
(2)
を
y(0)==1
として、0<x<2Pi の間で数値的に解いてグラフを描け．
Θ=Pi-.01;
Θ=πの位置は特異点である．その近くでの振り子の振る舞いを数値計算して見てみることにする．
In[18]:=
In[19]:=
Out[19]=
In[20]:=
Out[20]=
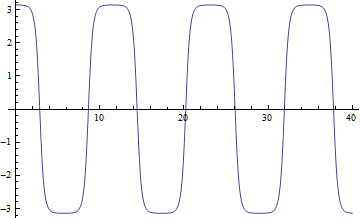
Θ=n πのところ（nは整数）ではあまり激しく動いていないことが読みとれる．相空間図は
In[21]:=
Out[21]=
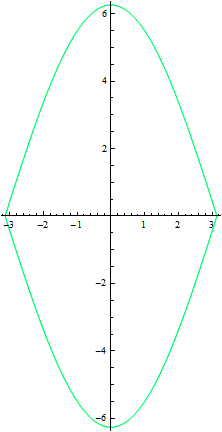
となる．上の図と一緒に描く．
In[22]:=
Out[22]=
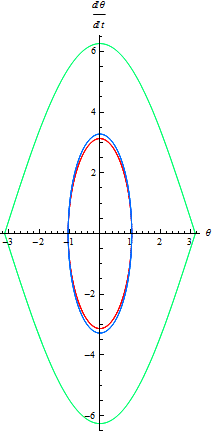
問６ Θ=Pi のときは不安定な平衡点と呼ばれる．何が起こるか？
問７ Θ=Pi 、 Θ=Pi+ 0.00000001 や Θ=Pi- 0.00000001 のときなどの数値計算をして運動の様子を調べ考察し、自分の意見（不安定な平衡点に対する認識とコンピュータによる数値計算法の良さや限界についてを述べよ．
周期
振り子の運動方程式は、
と書ける．両辺に
をかけt について積分すると
t=0のとき，θ==
，
=0 とすると
したがって周期τ は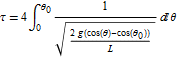
を計算すればよい。
In[23]:=
として
の値を0からπまで変化させて周期τを計算する。時間がかかるので数度に分けて計算してみよう．
In[25]:=
In[26]:=
Out[26]=
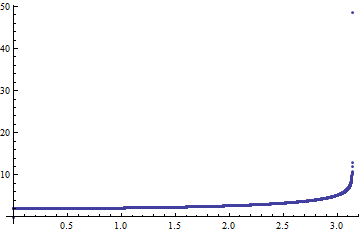
これではπに近づいたときの様子が詳しくわからないので，
In[27]:=
In[28]:=
In[29]:=
Out[29]=
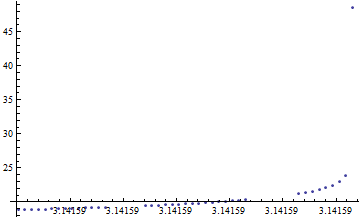
In[30]:=
Out[30]=
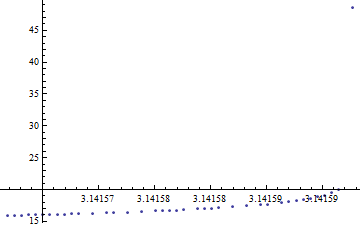
In[31]:=
Out[31]=
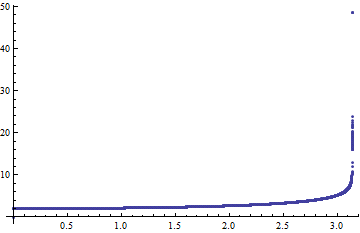
問８ 初期角度
がπに近づいたとき周期τはどのように振る舞うか？
